6. 有名なモデル
さて,一通り基本的なことは学んだので.有名なSNNモデルを紹介します.
私の知識の偏りにより,詳しく説明できるモデルが限られますのでご了承ください.
本サイトでは,2015年に提案されたモデルDiehl&Cookモデルを紹介します.
6-1. Diehl&Cook (2015)
Diehl&Cookモデル [13]は,教師なしSTDP学習モデルとして有名なモデルです.
なぜ有名なのかと言うと,STDP学習を核としてここまで上手く学習できるモデルは少ないからです.
まずはじめにネットワーク構成をお見せします.
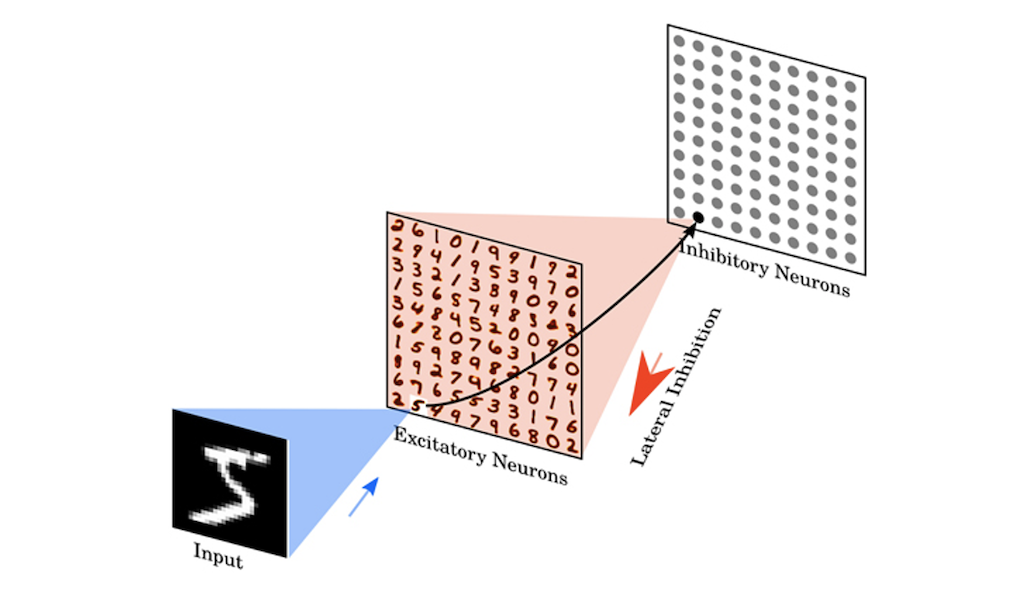
入力層,興奮性層,抑制性層のシンプルな3層構成です.
興奮性層は出力層にあたり,抑制性層は側抑制(Winner-take-all)にあたります.
ここで側抑制とは,一つのニューロンが発火した時,周りのニューロンの発火を抑制する作用を指します.
Winner-take-all(勝者総取り方式)とも言います.
ですのでこのネットワークは,2層構造とも捉えることができます.
本モデルの学習は以下の4つの柱によって成り立っています.
- STDP学習
- 側抑制
- Adaptive Threshold
- 重みの正規化
上の2つは既に説明したので良いでしょう.
残りの2つについて説明します.
まずAdaptive Thresholdですが,その名の通り動的に発火閾値が変化する機構です.
Diehl&Cookモデルでは,LIFモデルを用いていますがこの機構と合わせて,Adaptive LIFモデルと言われることがあります.
本機構により,ニューロンの発火閾値$V_{\theta}$は以下の式で変化します.
$$V_{\theta} = \theta_{0} + \theta(t)$$ $$\tau_{\theta}\frac{d\theta(t)}{dt} = -\theta(t) + \alpha\cdot s(t)$$
ここで,$\tau_{\theta}$は時定数,$\alpha$は増加定数です.
すなわち,発火閾値は発火すればするほど大きくなっていき,時間が経つにつれて自然減衰していきます.
これがDiehlらが提案しているAdaptive Thresholdです.
そして,重みの正規化ですが,これは入力層と興奮性層の間のシナプスで行われます.
さらに具体的に言うと,入力層ニューロン$28\times28$から一つの興奮性層ニューロンにつながるシナプス784個の中でL1正規化が行われます
ややこしいですね.
これは,重みが発散しないように全体的に押さえ込んでいるイメージになります.
とりあえずここまでの話を踏まえて学習する様子を見てみましょう.
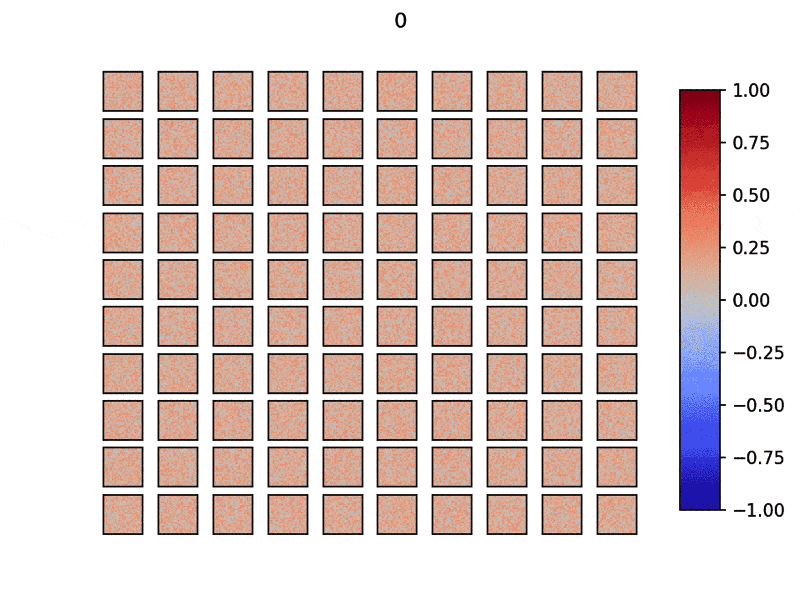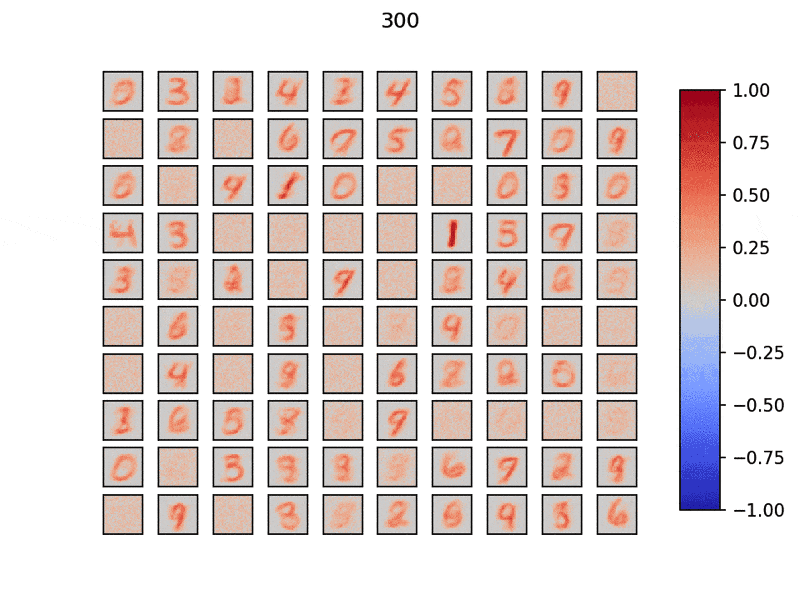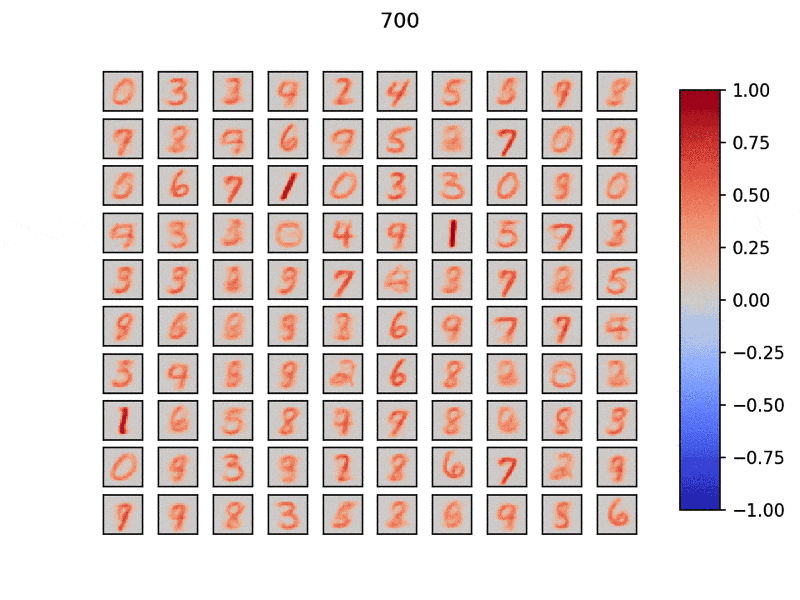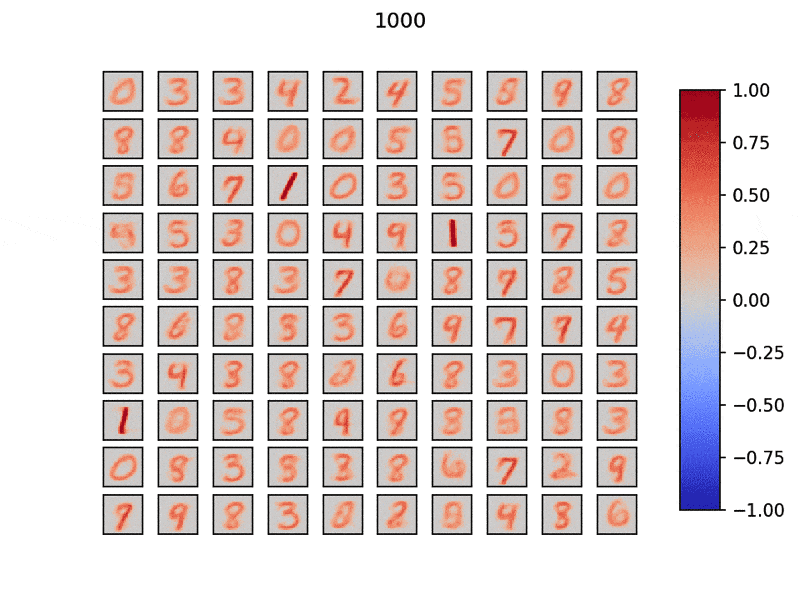
ひとつひとつのウィンドウは$28\times28$で計100個の興奮性ニューロンを用意しました.
タイトル部分は学習データ数で,MNISTデータセットを学習させています.
分散して入力データの特徴を素早く学習できていることがわかります.
さて,このモデルの学習をもう少し紐解いてみます.
興味ない方は飛ばしてください.
まず学習の柱として4つの機構を紹介しました.
STDP学習則については特に何の問題もありませんが,その他の3つの機構が大きな役割を持っています.
まずは,側抑制です.
側抑制は,発火したニューロン以外のニューロンを抑制する機構.
すなわち各ニューロンが独自の特徴を学べるようにしています.
ちなみにモデルの実装ではかなり大きめの側抑制値が設定されています.
次にAdaptive Thresholdは一つのニューロンが学習を独占しないようにする意図があります.
これらが無いとどうなるのでしょうか?
見てみましょう.
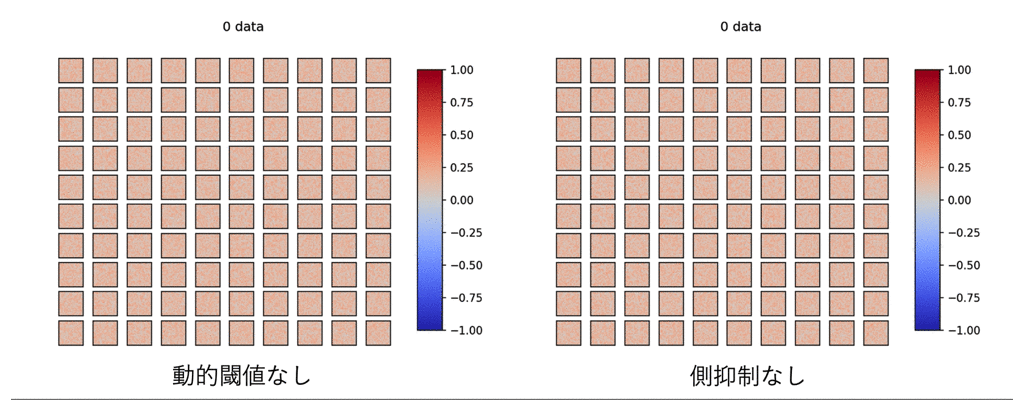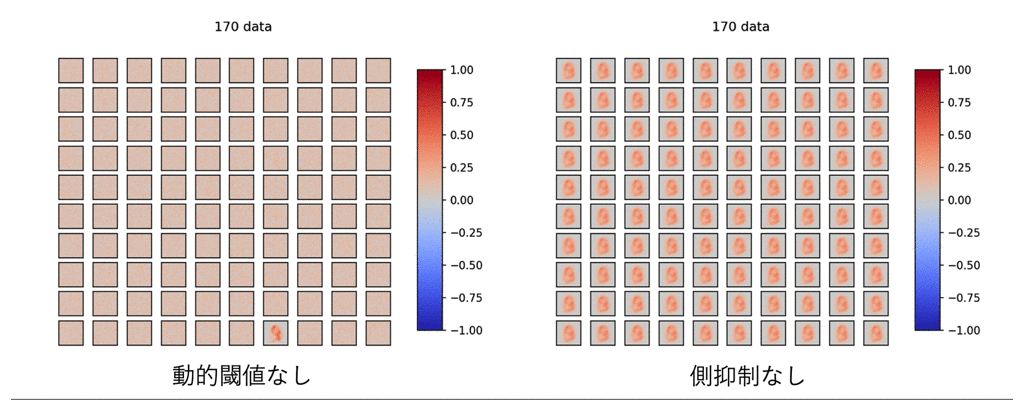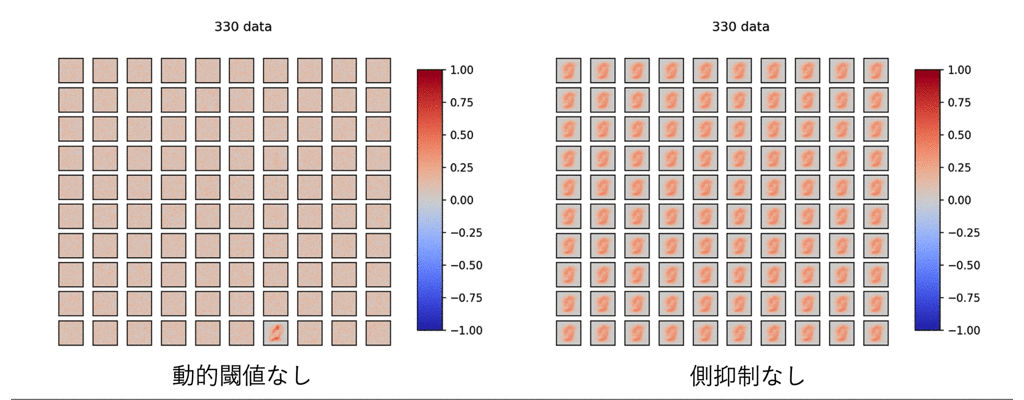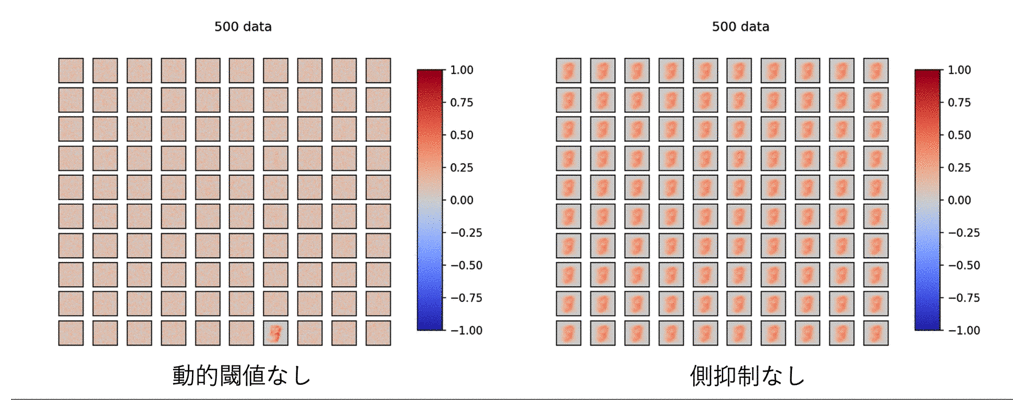
ひどい有様です.
これを見て,前章で言った「STDP単体ではどうにもならない」理由がわかると思います.
STDP学習はあくまでローカルな学習則であり全体を見ることはできません.
外部から,STDP学習を補助してあげないと何かを学習することは困難です.
と,色々と創意工夫が詰まったこのモデルですが,紐解くと結局STDP学習ベースの学習方法はなかなか難しいです.
本モデルは比較的STDP学習をそのまま使用した綺麗なモデルなので有名にはなりましたが,多くの課題が残ったままです.
後続研究もたくさんありますが,例えば以下のような後続研究が考えられます.
- 多層にする
- 畳み込み層を導入する
- 抑制性ニューロンも学習させる
などなど...
6-2. Liquid State Machine (2004)
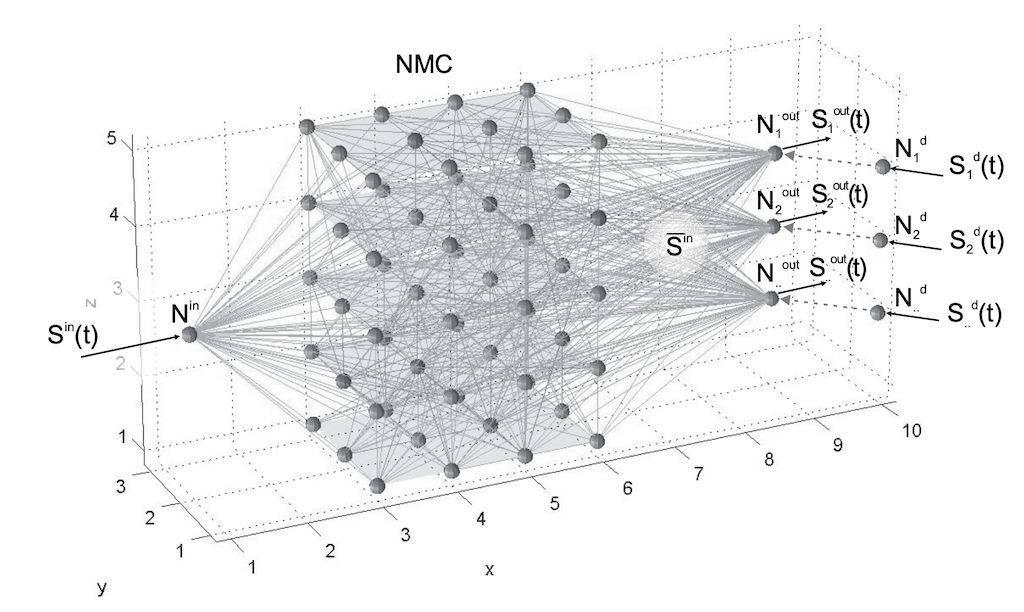
Liquid State Machine(LSM) [14]はリザーバコンピュータ(Reservoir Computer)の一種です.
リザーバコンピュータとは,入力層と出力層の間にリザーバ層と呼ばれるランダムに相互結合された中間層が設けられたニューラルネットワークのことです.
さらにそのリザーバ層の結合は,基本的にランダムに初期化されたまま学習はおこなわれません.
LSMはそのSNN版と考えて良いでしょう.
正直私は詳しく無いので先ほどのモデルよりかなり簡潔な紹介になってしまいますが,有名なモデルなので一応紹介することにしました.
実は,前章で軽く出てきたReSuMeもLSMを対象に実験を行っていました.
処理自体複雑で実装するのも難しいですが,我々の脳内のようなブラックボックスな状態を表現したモデルなので色々な研究で用いられています.
