5. 学習則
一番最後の大事な要素,それは学習則です.
ANNの学習則はHebb則から始まり,今は1986年に提案された誤差逆伝播学習法 [7] という超強力な学習法によって私たちの身の回りの利便性は作られています.
一方でSNNではどうでしょうか?
実際のところ,SNNには誤差逆伝播学習法のような強力な学習法はまだ存在しません.
誤差逆伝播学習法の要とも言える,勾配降下法という手法は教師信号と実際の出力結果の間に生じた誤差を微分して勾配を求めることで, 「どの程度内部を変更するか」を決定しています.
しかし,SNNはスパイク列という{0,1}の離散的なデータを情報としていますので,この勾配が簡単には計算できないのです.
ではSNNを学習する方法は何なのか.
本章はそこに焦点を当てて話していきます.
5-1. STDP学習則
SNNで最もよく用いられる学習則が,STDP(Spike-timing-dependent plasticity)学習則 [8]です.
日本語では,スパイクタイミング依存可塑性と訳されます.
STDP学習則は,1949年に発表された生物学的に妥当性のある学習則であるHebb則が,より精緻に観測されたものと言われています.
Hebb則は「2つのニューロンが同時に発火した時その間のシナプス結合は強化される」というものでしたが, STDP学習則は「2つのニューロンの発火時刻差に依存したシナプス結合強化が行われる」というものです.
STDP学習には,対象型と非対称型がありますが,本節ではメジャーな非対称型について見ていきます.
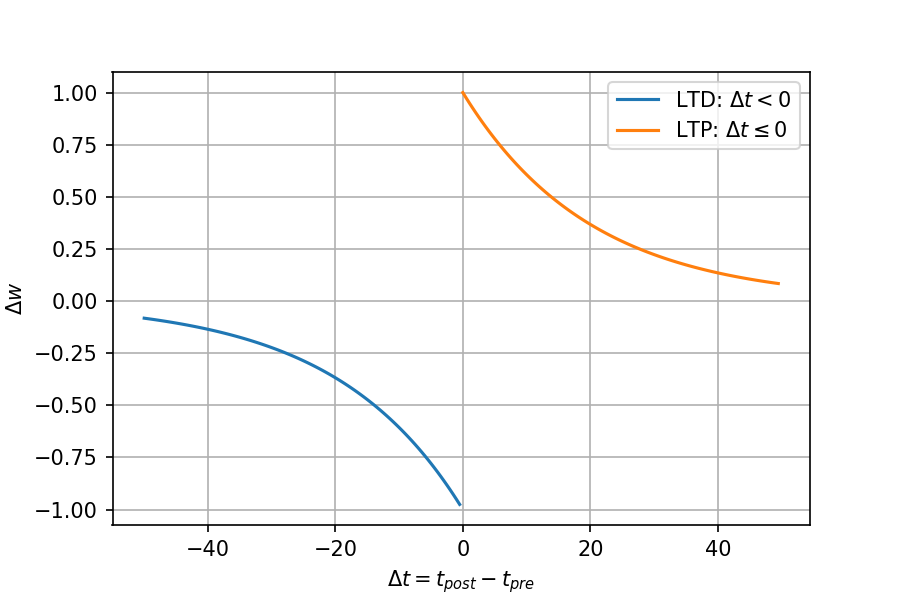
最初に,STDP学習則の式とグラフを示します.
$$\Delta w= \begin{cases} A_{+}\exp(-\Delta t / \tau_{+}), \ \ &{\rm if}\ \ \Delta t \geq 0 \\ A_{-}\exp( \Delta t / \tau_{-}), \ \ &{\rm if}\ \ \Delta t < 0 \end{cases}$$ $${\rm where}\ \ \Delta t = t_{post} - t_{pre}$$
import numpy as np
import matplotlib.pyplot as plt
def stdp_ltp(dt, a=1.0, tc=20):
""" Long-term Potentiation """
return a * np.exp(-dt / tc)
def stdp_ltd(dt, a=-1.0, tc=20):
""" Long-term Depression """
return a * np.exp(dt / tc)
def stdp(dt, pre=-1.0, post=1.0, tc_pre=20, tc_post=20):
""" STDP rule """
return stdp_ltd(dt[dt<0], pre, tc_pre), stdp_ltp(dt[dt>=0], post, tc_post)
if __name__ == '__main__':
# 発火時刻差集合
dt = np.arange(-50, 50, 0.5)
# LTD, LTP
ltd, ltp = stdp(dt)
plt.plot(dt[dt<0], ltd, label=r'LTD: $\Delta t < 0$')
plt.plot(dt[dt>=0], ltp, label=r'LTP: $\Delta t \leq 0$')
plt.xlabel(r'$\Delta t = t_{post} - t_{pre}$')
plt.ylabel(r'$\Delta w$')
plt.grid()
plt.legend()
plt.show()STDPはシナプス長期増強(LTP: Long-term Potentiation)と,シナプス長期抑圧(Long-term Depression)に分けられます.
前ニューロンの発火時刻を$t_{pre}$,後ニューロンの発火時刻を$t_{post}$としたときの時刻差$\Delta t$によって重みの更新量が決定します.
発火時刻差が小さいほど更新量は大きくなるところはHebb則と近い考えですが, 後ニューロンの発火に前ニューロンの発火が起因したか否かで更新量のプラスかマイナスが決定します.
$\Delta t=0$の時の更新量は$0$としてしまうときもありますが,実世界では基本的にそんなことは無いので論文によりますね.
$A_+$と$A_-$はスケーリング係数ですが,学習率と同じです.
ここからは,STDP学習を実装する場合の話ですが,実際にスパイク一本ずつ精査していたら無駄なので,よくトレース(Trace)という考え方が用いられます.
トレースには,2種類あります.
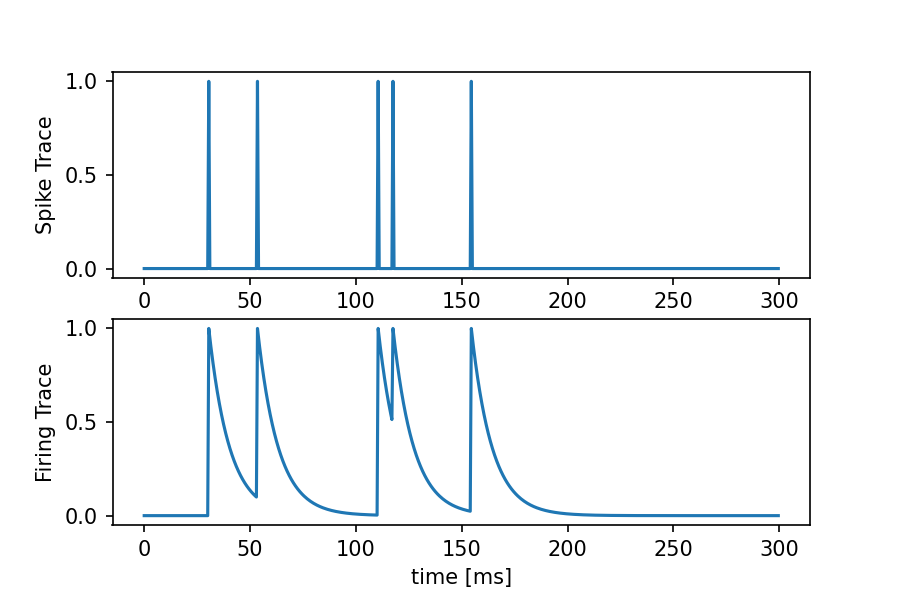
- スパイクトレース(Spike Trace) ... {0,1}のただのスパイク列を記録したもの
- 発火トレース(Firing Trace) ... [0, 1]の時間的減衰をつけたスパイク列
の2つです.
わかりづらいので,実際に描画してみるとこのような感じです.
import numpy as np
import matplotlib.pyplot as plt
if __name__ == '__main__':
time = 300
dt = 0.5
# Spike Traceを適当に作る
spikes = np.zeros(int(time/dt))
# 5本適当にスパイクを立てる
for _ in range(5):
spikes[np.random.randint(0, int(time/dt))] = 1
# Firing Traceを作成
firing = []
fire = 0
tc = 20 # 時定数
for t in range(int(time/dt)):
if spikes[t]: # 発火していれば1を立てる
fire = 1
else: # 発火していなければ時間的減衰
fire -= fire / tc
firing.append(fire)
t = np.arange(0, time, dt)
plt.subplot(2, 1, 1)
plt.plot(t, spikes, label='Spike Trace')
plt.ylabel('Spike Trace')
plt.subplot(2, 1, 2)
plt.plot(t, firing)
plt.ylabel('Firing Trace')
plt.xlabel('time [ms]')
plt.show()前ニューロンの各トレース,後ニューロンの各トレースを,それぞれ$X_{pre}^{s}, X_{pre}^{f}$ そして$X_{pre}^{s}, X_{post}^{f}$と表した時, STDP学習は以下のように計算できます.
- $\Delta w_{LTD} = A_{-}(X_{pre}^{s}\cdot X_{post}^{f})$
- $\Delta w_{LTP} = A_{+}(X_{pre}^{f}\cdot X_{post}^{s})$
これもイメージがつきづらいかもしれませんが,スパイクトレースは発火しているか否か,発火トレースは実際のSTDP更新量を示しています.
STDP学習はLTDもLTPもどちらかの発火時刻を基準に更新量を決定しているわけですから,上記のようなベクトル内積計算で全てのスパイクについて,一度で更新量を計算できます.
ところで「ぶっちゃけこれだけで何かを学習できるの??」と思う方もいるでしょう.
答えは「できません」.
語弊があるかもしれませんが,STDP学習則はあくまで記憶形成のための学習則の一つに過ぎません.
他の学習のための工夫があって,やっと何かを学習できる形態になります.
これについては次章で例を挙げて紹介します.
5-2. 勾配降下法ベース
他にも,SNNの学習方法には「どうにか強力な勾配降下法を適用させたい」という思想のもと提案されたものがあります.
なんたって,誤差勾配が求まれば学習ができるということは自明なわけですから,いかに「誤差勾配」を近似的に求めるかが勝負な研究分野です.
なぜ勾配を求めるのが難しいかというと,最初に言ったように,出力発火時刻と重みは簡単な関数では表すことができず離散的な情報だからです.
これに当たる手法はいくつかありますので一気に,簡潔に紹介します.
いずれも基本は,実際の出力発火時刻$t^a$と教師発火時刻$t^d$を用いて,
$$E=\frac{1}{2}\sum(t^d-t^a)^2$$
$$\Delta {\mathbf w} = \frac{\partial E}{\partial {\mathbf w}} = ...$$
という誤差関数の勾配($w$による偏微分)をいかにうまく計算するかを鍵としています.
もし,気になる手法があればぜひ論文を読んでみてください.(私は全て真面目に読んだわけではありません)
- Spike-Prop (2000)(2002) [9] [10]
... (おそらく)元祖SNN勾配降下法.発火時刻$t^a$は内部状態の関数だと見立てて勾配を計算している手法. 連鎖率をうまく利用しつつ,しっかり線形分離不可能な問題も解けるということで,SNN界隈では有名なモデル. - NormAD (2015) [11]
...Normalized Approximate Decentの略で,出力スパイク列から近似的に膜電位を算出して,膜電位誤差から勾配を求める手法. やや癖がある手法であまり有名な手法ではないが,個人的には面白いと思う. 2015年の論文では最終層しか学習できず課題になっていたが,最近多層にも対応できたらしい? - ReSuMe (2005) [12]
...Remote Supervised Methodの略. 勾配降下法ベースではないが,教師あり学習に分類される.更新量はSTDP学習則をもとに作られたLearning Windowを用いる. SNN教師あり学習のなかでは有名な手法の一つ.
と,いくつか紹介しましたが,私個人の意見としては誤差逆伝播学習法をSNNに適用させるのは,好ましく無いアプローチかなと思います.
そもそも,誤差逆伝播学習法のような大掛かりな逆伝播処理は我々の脳内では行われていないですし, そう考えると,良い結果を得られたとしてもSNNであるメリットって何だろうと考えてしまいます...
SNNの研究を工学的な立ち位置でやるのか,それとも生物学的な立ち位置でやるのか,というのを最初に決めておくのが良いと思います.
ここで言うそれぞれの立ち位置は,
- 工学的立ち位置 ... とりあえず精度と実用性.生物学的妥当性は二の次.
- 生物学的立ち位置 ... 生物学的妥当性を最優先.
だと私は考えています.
これから,SNNについて研究しようとしている方は,一度立ち止まって「自分はどちらの立ち位置につくか」を少し考えてみてください.
もちろん,両方大事という気持ちもわかりますが,いつかジレンマに陥る可能性は十分あり得ます.
