4. エンコーディング
SNNを理解する上で大事な要素としてエンコーディング(Encoding)があります.
主に工学的なモデルを実装する際に大事になってくる話ですが,要は実世界の情報をどうやってスパイク列に変換するかです.
レートエンコーディング(Rate-Encoding)とも言います.
また,スパイク列を実世界の情報に変換する作業をデコーディング(Decoding)と言います.
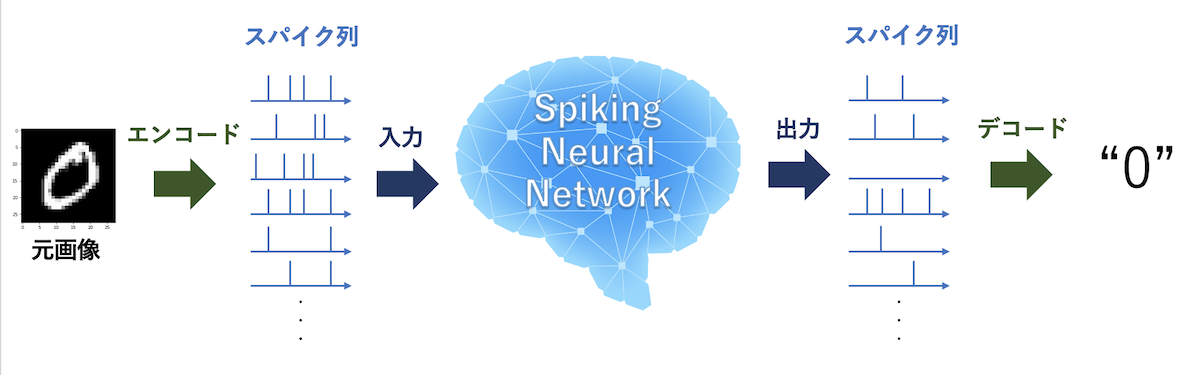
デコーディングは,あらかじめニューロンに役割を決めておいて一番発火したニューロンが勝ち,のようなシンプルなアイデアが思いつくのですが, エンコーディングはイメージが湧かない人が多いのではないでしょうか?
いくつか方法がありますが,ここでは代表的なものを紹介していきます.
4-1. ポアソンエンコーディング
最もよく用いられるものが,ポアソン過程(Poisson Process)に従った方法です.
ポアソン過程やポアソン分布は確率統計でよく用いられる考えです.
定義は以下の式から成り立ちます.(証明は割愛)
$$P(X=k) = \frac{\lambda^{k}\exp(-\lambda)}{k!}$$
この式が表すことは,
- ある時間中に平均$\lambda$回起こる事象が$k$回起こる確率
です.
もっと現実世界に沿った言い方をしましょう.
- 1年間に平均100日雨の日があるとして,雨の日が1年間で90日の確率は?
のような使い方です.
もちろん,100日になる確率が一番多く,そこから離れるに従って確率は下がっていきます.
至極当たり前な確率分布がポアソン分布です.
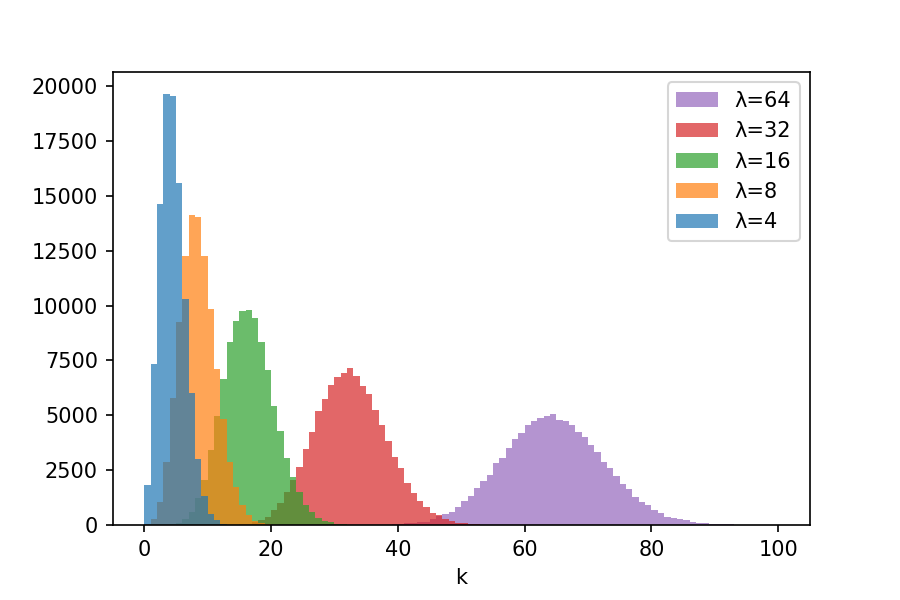
実際に確率分布を見てみましょう.
import numpy as np
import matplotlib.pyplot as plt
if __name__ == '__main__':
num = 100000 # 抽出回数
lam = [4, 8, 16, 32, 64] # lambda
res = [np.random.poisson(l, num) for l in lam] # Poisson dist. から抽出
plt.hist(res, bins=100, histtype='stepfilled', alpha=0.7)
plt.xlabel('k')
plt.legend([f'λ={l}' for l in reversed(lam)])
plt.show()$\lambda$が大きくなるにつれて,正規分布のようになっていくこともわかります.
ポアソン分布の特徴として,整数しか取らないこともあげられます.
さて,エンコーディングの話に戻ります.
我々の脳内では,外部から刺激がないときにも自発的な発火が行われています.
例えば寝ている時も,脳内では何かしらの処理が絶えずなされているわけです.
そのときの,発火頻度がポアソン過程に従っていると言われています.
正確には,次の発火までの時間,すなわち周期がポアソン過程に従っていると言われています.
そういった意味で,ポアソン過程は生物学的妥当性を持ち,SNNにおいてエンコーディング処理としてよく用いられます.
正直,自発的発火とエンコーディングは関係がない気はするのですが,このあたりも研究課題ですね.
このポアソン過程に沿ってエンコードする方法を,ポアソンエンコーディング(Poisson Encoding) [5]と呼ぶこともあります.
ポアソンエンコーディングについて手順を見ていきましょう.
- 実数値情報を周波数 [Hz]に変換(正規化)する
- 周波数を周期$\lambda$ [ms]に変換する
- 周期$\lambda$をもとに次の発火までの時間$k$ [ms]を抽出する
といった手順を踏みます.
言葉だけだとよくわかりませんね.
適当に小さな画像を例に変換例を見てみましょう.
import numpy as np
import matplotlib.pyplot as plt
if __name__ == '__main__':
max_freq = 128 # 最大スパイク周波数 [Hz] = 1秒間 (1000 ms) に何本のスパイクを最大生成するか
time = 300 # 観測時間 [ms]
dt = 0.5 # 時間分解能 [ms]
image = np.random.random((3, 3)) # 適当な画像
freq_img = image * max_freq # pixels to Hz
norm_img = 1000. / freq_img # Hz to ms
norm_img = norm_img.reshape(-1) # 2次元だと扱いが面倒なので1次元に
spikes = [
# 周期が抽出されるのでスパイク発生時間としては累積させなければならない
# とりあえず,今回は約300msに収まる分だけ抽出
np.cumsum(np.random.poisson(cell / dt, (int(time / cell + 1)))) * dt
for cell in norm_img
]
# Plotting
plt.figure(figsize=(10, 4))
# Original Image
plt.subplot(1, 2, 1)
plt.title('original')
plt.imshow(image, cmap='gray')
plt.xticks([])
plt.yticks([])
plt.colorbar()
for num in range(9):
plt.text(int(num%3), int(num/3), str(num), color='tab:blue', fontsize=14)
# Spike trains generated by Poisson Encoder
plt.subplot(1, 2, 2)
plt.title('Spike firing timing')
for i, s in enumerate(spikes):
plt.scatter(s, [i for _ in range(len(s))], s=1.0, c='tab:blue')
plt.xlim(0, time)
plt.ylabel('pixel index')
plt.xlabel('time [ms]')
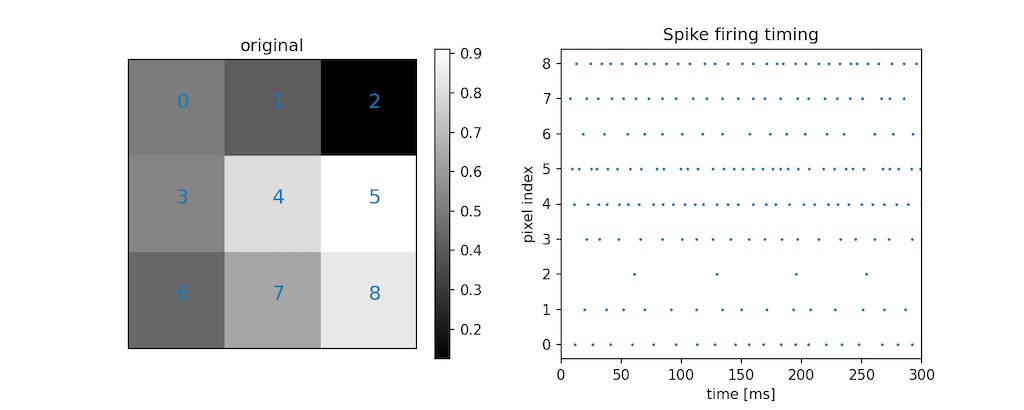
plt.show()左の3x3のランダムな画像を元に,ポアソンエンコーディングによって生成されたスパイク列が右図です.
スパイクの有無をラスター図としてプロットしています.
画素値番号が,右図の縦軸とリンクしています.
生成されたスパイク列を見ると,画素値が小さいほど疎なスパイク列で,画素値が大きいほど密なスパイク列が生成されています.
また,スパイク同士の感覚はおおよそ同じです.
というのも,スパイクの間隔はポアソン分布によって確率的に抽出されているわけですから,おおよそ同じなのです.
ところで,なぜ一旦「周波数」に変換したかわかりましたか?
ダイレクトに周期に変換しても良いのですが,周波数は言わば1秒間に何本のスパイクが立つかを表しているので, 変換前の実数値の大きさとスパイクの密度をリンクさせるためには周波数で考えた方がわかりやすいですよね.
4-2. ニューラルエンコーディング
さて,他にもエンコード方法はあります.
それは,実際のニューロンの処理に基づいてエンコーディングする方法です.
もしかしたら,こちらの方がイメージがつきやすいかもしれません.
要は実数値情報をそのまま入力電流に変換して,エンコーディング用のニューロンに入力してその出力スパイク列を扱う,ということです.
やり方は様々あるかと思いますが,とある論文 [6]では以下のような変換式を用いていました.
$$I(t) = I_{0} + (k\times I_{p})$$
ここで,$I_{0}$は発火しないギリギリの電流値で,$k$は画素値,$I_{p}$は倍率です.
こちらのエンコードは研究によってやり方は様々ですが,あまりエンコードに関する論文が少なく,そもそもエンコード方法に言及している論文もなかなか無いので実態はよくわかりません.
4-3. 実装例
ここまで学んだことを組み合わせて実装してみます.
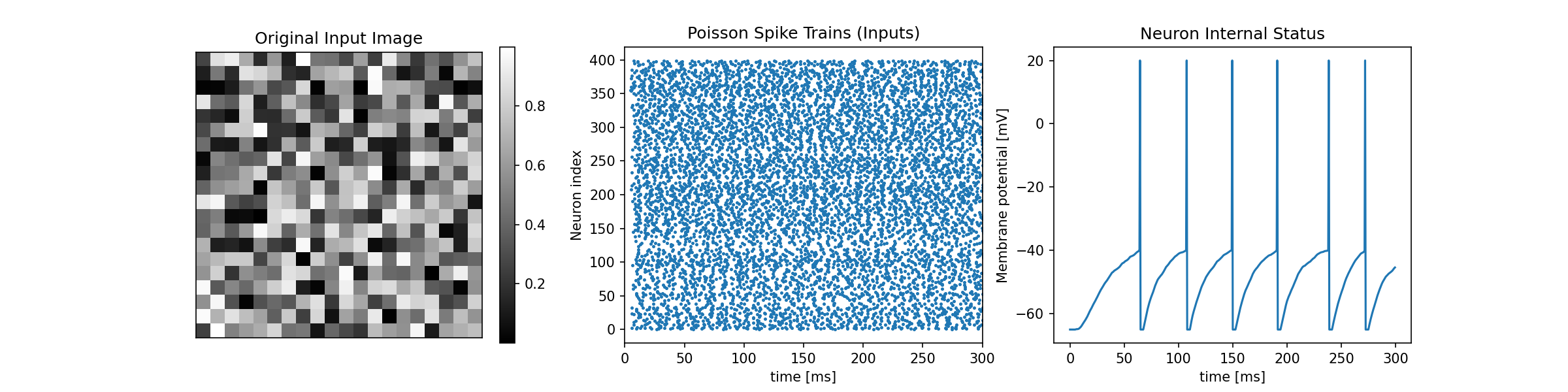
実装条件は,
- $20\times 20$入力画像を入力とする (画像は乱数でもなんでも良い)
- LIFニューロンからなるIn(400) - Out(1)の超シンプルなSNN
- ネットワークの重みは適当に乱数で初期化 (確率分布は任意)
- 出力は①元画像,②入力スパイク列,③出力層ニューロンの膜電位を描画
です.
かなりシンプルなものですが,SNNの簡単なサンプルとしては適量です.
それぞれの素材はすでに学習したものですので,なんとなく実装の仕方は思いつくと思いますが, ポアソン過程によって得られた発火時刻を,どのように{0,1}のスパイク列に変換するか,は個人差が出そうですね.
とりあえず,私の実装例を出力結果例とともにお見せします.
import numpy as np
import matplotlib.pyplot as plt
class LIF:
def __init__(self, rest: float = -65, ref: float = 3, th: float = -40, tc: float = 20, peak: float = 20):
"""
Leaky integrate-and-fire neuron
:param rest: 静止膜電位 [mV]
:param ref: 不応期 [ms]
:param th: 発火閾値 [mV]
:param tc: 膜時定数 [ms]
:param peak: ピーク電位 [mV]
"""
self.rest = rest
self.ref = ref
self.th = th
self.tc = tc
self.peak = peak
def calc(self, inputs, weights, time=300, dt=0.5, tci=10):
"""
膜電位を計算する.
本来はスパイク時刻(発火時刻)も保持しておいてそれを出力データとする.
:param inputs:
:param weights:
:param time:
:param dt:
:param tci:
:return:
"""
i = 0 # 初期入力電流
v = self.rest # 初期膜電位
tlast = 0 # 最後に発火した時刻
monitor = [] # 膜電位の記録
for t in range(int(time/dt)):
# 入力電流の計算
di = ((dt * t) > (tlast + self.ref)) * (-i)
i += di * dt / tci + np.sum(inputs[:, t] * weights)
# 膜電位の計算
dv = ((dt * t) > (tlast + self.ref)) * ((-v + self.rest) + i)
v += dv * dt / self.tc
# 発火処理
tlast = tlast + (dt * t - tlast) * (v >= self.th) # 発火したら発火時刻を記録
v = v + (self.peak - v) * (v >= self.th) # 発火したら膜電位をピークへ
monitor.append(v)
v = v + (self.rest - v) * (v >= self.th) # 発火したら静止膜電位に戻す
return monitor
if __name__ == '__main__':
time = 300 # 実験時間 (観測時間)
dt = 0.5 # 時間分解能
image = np.random.random((20, 20)) # 適当な画像
max_freq = 128 # 最大スパイク周波数 [Hz] = 1秒間 (1000 ms) に何本のスパイクを最大生成するか
freq_img = image * max_freq # pixels to Hz
norm_img = 1000. / freq_img # Hz to ms
norm_img = norm_img.reshape(-1) # 2次元だと扱いが面倒なので1次元に
fires = np.array([
# 周期が抽出されるのでスパイク発生時間としては累積させなければならない
# とりあえず,今回は約300msに収まる分だけ抽出
np.cumsum(np.random.poisson(cell / dt, (int(time / cell + 1)))) * dt
for cell in norm_img
])
# 発火時刻→スパイク列
spikes = np.zeros((norm_img.size, int(time/dt)))
for s, f in zip(spikes, fires):
f = f[f < time] # 300msからはみ出た発火時刻は除く
s[np.array(f / dt, dtype=int)] = 1 # {0,1} spikesへ変換する
# 重みの初期化 (適当に)
weights = np.random.normal(0.1, 0.4, norm_img.size)
# LIFニューロンの生成および膜電位計算
neuron = LIF()
v = neuron.calc(spikes, weights, time, dt)
# 結果の描画
plt.figure(figsize=(16, 4))
# 入力画像
plt.subplot(1, 3, 1)
plt.title('Original Input Image')
plt.imshow(image, cmap='gray')
plt.xticks([])
plt.yticks([])
plt.colorbar()
# 入力データ
plt.subplot(1, 3, 2)
t = np.arange(0, time, dt)
for i, f in enumerate(fires):
plt.scatter(f, [i for _ in range(len(f))], s=2.0, c='tab:blue')
plt.xlim(0, time)
plt.xlabel('time [ms]')
plt.ylabel('Neuron index')
plt.title('Poisson Spike Trains (Inputs)')
# 膜電位
plt.subplot(1, 3, 3)
plt.plot(t, v)
plt.xlabel('time [ms]')
plt.ylabel('Membrane potential [mV]')
plt.title('Neuron Internal Status')
plt.show()SNNをコーディングする際に何が大変かと言うと,時間は整数じゃないということです.
しかしスパイク列のインデックスは整数でなければいけないので,スパイク列や膜電位の計算は$T/dt$で考えなければいけませんし, 発火時刻は浮動小数点のまま考えなければいけません.
この相互変換が頭を悩ませるポイントだったりします.
コード中でも,
* dtしていたり
/ dt
していたりと,ところどころに相互変換が見受けられると思います.
今回の単純パーセプトロンのような小さなSNNでもなかなかの計算量ですね.
シミュレーションでは,ここにさらに学習も入るわけですから,実装も一筋縄ではいきませんね.
さて,次章は今少しだけ触れた学習について話していきます.
