3. 神経細胞のモデル化
ここからが本サイトの核と言っても過言ではありません.
神経細胞の数理モデル化についてです.
現在主流のニューロンモデルは,形式ニューロンモデル(McCulloch&Pittsモデル) [1]をベースにしたものです.
形式ニューロンモデルは現在主流と言えど,本来の神経細胞の挙動とは大きな乖離があります.
それは,形式ニューロン自体が1943年に発案されたということもあり,かなり簡易なモデルだからです.
時間次元も持っていない簡素なモデルですが,簡易だからこそ扱いやすく応用の幅が効きますので現在も主流なモデルとして利用されているのです.
3-1. 形式ニューロンモデル
スパイキングニューラルネットワークとはあまり関係がありませんが,一応本モデルについても触れておきます.
形式ニューロンのコンセプトは以下の特徴を組み込んだモデルであることです.
- 他細胞からの入力を積和する
- その結果がある閾値を超えたら1そうでなければ0とする (発火を表現)
これだけです.
式に表すと,
$$y=\sum_{i\in N}{w_i x_i}$$ $$z=f(y-b)$$ $$f(X)=\begin{cases} 1, \ \ {\rm if}\ \ X>0 \\ 0, \ \ {\rm if}\ \ X\leq0 \end{cases}$$
のシンプルな3式です.
以上の式を図で表すと以下のような感じです.
ちなみに$b$はバイアスで,発火閾値に当たります.
$N$はシナプス前ニューロンの集合で,$w$はシナプス結合荷重(重み),$x$はシナプス前ニューロンの出力を表しています.
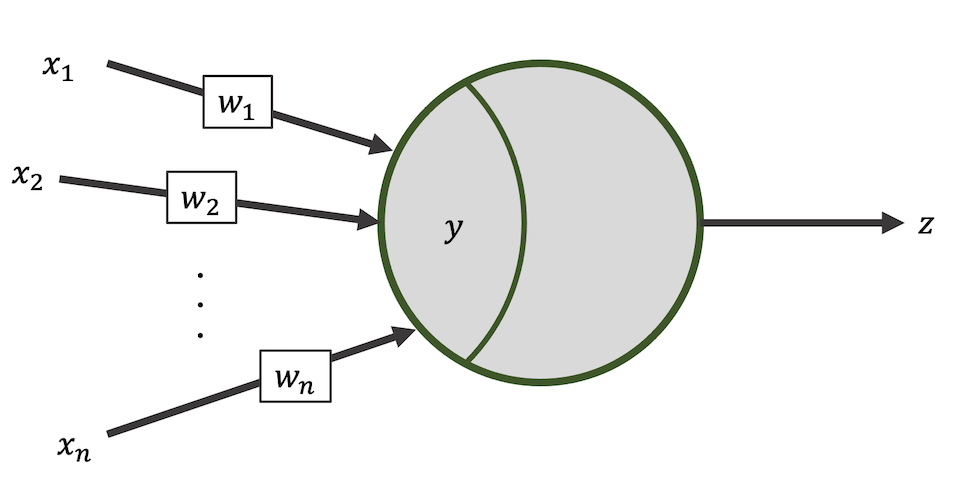
つまるところ,形式ニューロンモデルはある一時刻における発火の有無を見ているニューロンモデルです.
当初の形式ニューロンモデルは上の式であるように,発火の有無を表現するステップ関数を用いていましたが, 現在ではシグモイド関数やReLU関数など様々な入出力関数が使われています.
なぜなら,正直{0,1}の出力だけだと情報量が乏しいからです.
そして,強力な学習法である勾配降下法で勾配を計算するためです.
しかし,思い出してください.
本物の神経細胞は{0,1}のスパイク列で情報のやりとりをしています.
こういう意味で,現在主流のANNは本来の神経細胞との挙動と「乖離がある」と言ったのです.
3-2. LIFニューロンモデル
そこで,本来の神経細胞の挙動に近づけようとしたモデルを考えます.
まずは最もメジャーで比較的扱いやすいLIFモデル [2]を見ていきます.
LIFはLeaky integrate-and-fireの略で,日本語では漏れ積分発火モデルと訳されたりします.
最初に式を見てみましょう.
$$\tau_{m}\frac{dV(t)}{dt}=(-V(t) + E_{rest}) + I(t)$$
形式ニューロンとは形がだいぶ違うので戸惑うかもしれません.
ここで,$V(t)$は膜電位,$I(t)$は入力電流です.
$E_{rest}$ は静止膜電位で$\tau_{m}$は膜時定数と呼ばれる「漏れ」具合を制御する定数です.
膜電位$V(t)$がとある発火閾値$V_{\theta}$を超えた時,LIFニューロンは発火し,不応期に入ります.
ここまでの説明では,まだよく分からないと思いますので,実際に動作を見てみましょう.
適当なサインカーブの組み合わせを入力電流としてみます.
import numpy as np
import matplotlib.pyplot as plt
def lif(currents, time: int, dt: float = 1.0, rest=-65, th=-40, ref=3, tc_decay=100):
""" simple LIF neuron """
time = int(time / dt)
# initialize
tlast = 0 # 最後に発火した時刻
vpeak = 20 # 膜電位のピーク(最大値)
spikes = np.zeros(time)
v = rest # 静止膜電位
monitor = [] # monitor voltage
# Core of LIF
# 微分方程式をコーディングするときは,このように時間分解能dtで離散的に計算することが多い
for t in range(time):
dv = ((dt * t) > (tlast + ref)) * (-v + rest + currents[t]) / tc_decay # 微小膜電位増加量
v = v + dt * dv # 膜電位を計算
tlast = tlast + (dt * t - tlast) * (v >= th) # 発火したら発火時刻を記録
v = v + (vpeak - v) * (v >= th) # 発火したら膜電位をピークへ
monitor.append(v)
spikes[t] = (v >= th) * 1 # スパイクをセット
v = v + (rest - v) * (v >= th) # 静止膜電位に戻す
return spikes, monitor
if __name__ == '__main__':
duration = 500 # ms
dt = 0.5 # time step
time = int(duration / dt)
# Input data
# 適当なサインカーブの足し合わせで代用
input_data_1 = 10 * np.sin(0.1 * np.arange(0, duration, dt)) + 50
input_data_2 = -10 * np.cos(0.05 * np.arange(0, duration, dt)) - 10
input_data = input_data_1 + input_data_2
spikes, voltage = lif(input_data, duration, dt)
# Plot
plt.figure(figsize=(12, 6))
plt.subplot(2, 1, 1)
plt.ylabel('Input Current')
plt.plot(np.arange(0, duration, dt), input_data)
plt.subplot(2, 1, 2)
plt.ylabel('Membrane Voltage')
plt.xlabel('time [ms]')
plt.plot(np.arange(0, duration, dt), voltage)
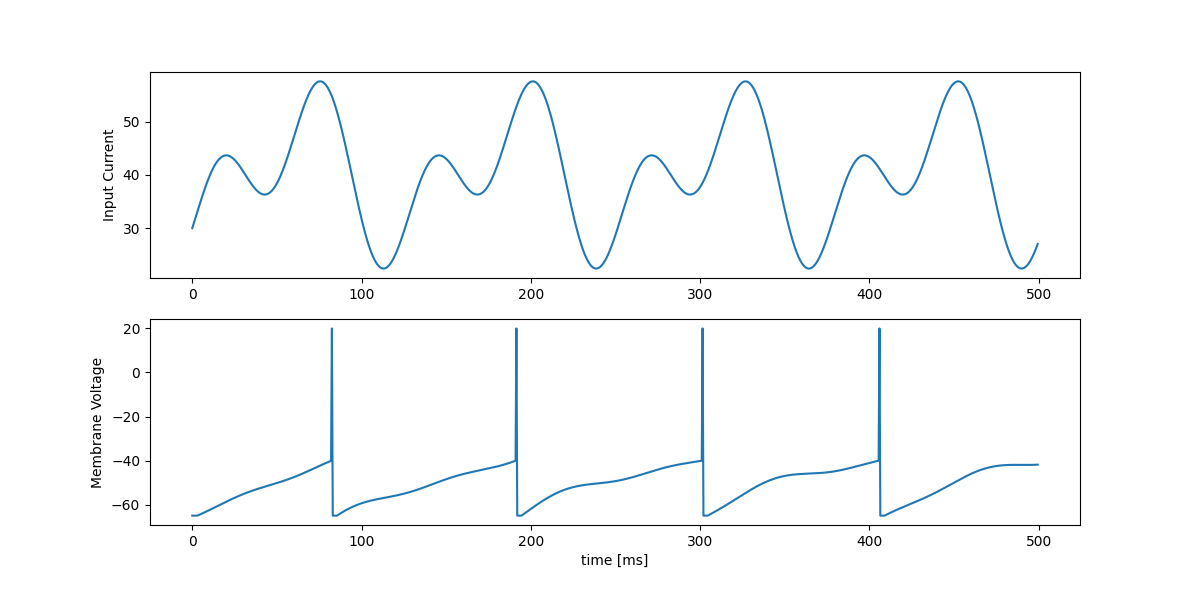
plt.show()このような挙動になります.
入力によって膜電位が変化して,発火閾値を超えると発火する,その挙動を表せていますね.
このとき発火した時刻や頻度,すなわちスパイク列が出力として,そしてニューロン同士のやりとりに使われます.
つまり,{0,1}の配列が入出力になるわけですね.
他細胞から受け取ったスパイク列をどのように入力電流$I(t)$に変換するかについては,本章最後に解説しようと思います.
さて,それよりもなぜこのような式になったのでしょうか?
- ここからは算出方法について書いていきますが,必要なければ次節に飛んでください.
まずは神経細胞の構造を思い出してみましょう.
神経細胞には,細胞膜があり膜電位が存在します.
またイオンチャネルによって各イオンの流入や漏れ(リーク)があります.
このことから,神経細胞の構造は一種の充電回路とみなせるわけです.
細胞膜がコンデンサのような働きをするわけですね.
単純な等価回路は以下のような形になります.
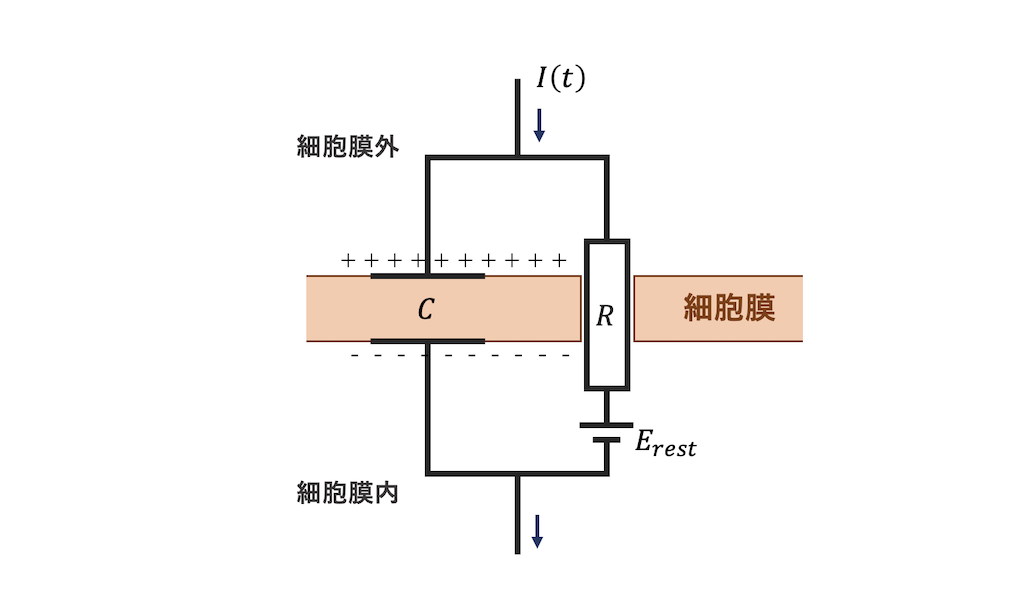
これをもとに式を立てるとLIFニューロンモデルの膜電位算出式が出来上がります.
まずは先の等価回路を以下のように考えます.
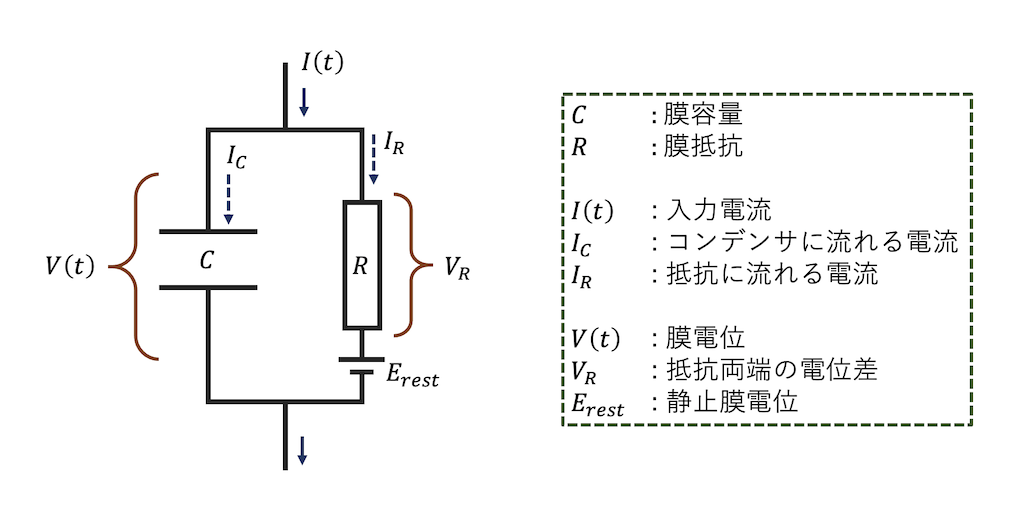
すると,キルヒホッフの第1法則と第2法則を用いて以下の式が出来上がりますね.
$$I(t) = I_{C} + I_{R} \ \ \ (1)$$ $$V(t) = V_{R} + E_{rest} \ \ \ (2)$$
次に,式(1)と(2)を組み合わせましょう.
さらにここで,$\tau_{m} = CR$とすると,
$$\tau_{m}\frac{dV(t)}{dt} = -(V(t) - E_{rest}) + RI(t) \ \ \ (3)$$
のように変形できました.
これでLIFモデルにおける膜電位算出式の出来上がりです.
入力電流の項にある$R$は重みと一緒にして省かれることも多いですが,正確には式(3)がLIFの算出式です.
3-3. Hodgkin-Huxleyニューロンモデル
次に,Hodgkin-Huxley(HH)モデル [3]について話していきます.
HHモデルは工学的な研究では扱われることは少なく,神経科学の解析や再現に多く使われるモデルです.
HHモデルは現存の数理モデルの中では最も細かくニューロンの挙動をモデル化したものになります.
ここでは詳細な解説はしませんが,一言で表すならば,
- イオンの流出入を細かく定義したモデル
です.
LIFモデルではイオンチャネルを一つにまとめて,単なるリークとしていましたが,HHではカリウムイオンチャネルとナトリウムイオンチャネルの挙動を別で定義することで再現性を高めています.
HHにおいて,膜電位の算出式は以下の10個の式から成り立ちます. (数式は横スクロール可能)
これだけでも,モデルの複雑性が伝わるかと思います.
$E_{X}$は$X$イオンの平衡電位で,$g_{X}$は$X$イオンの抵抗(単位は$[{\rm S}]=[{\rm R^{-1}}]$)を表しています.
$l$はLeakの頭文字です.
$n, m, h$は各チャネルの(不)活性化パラメータと呼ばれ,チャネルが開いている度合いを司ります.
その他の各定数は実際の実験で得られた値ですので,変化することは基本ありません.
(ヤリイカの巨大軸索を使って実験したそう)
実際に動作を見てみましょう.
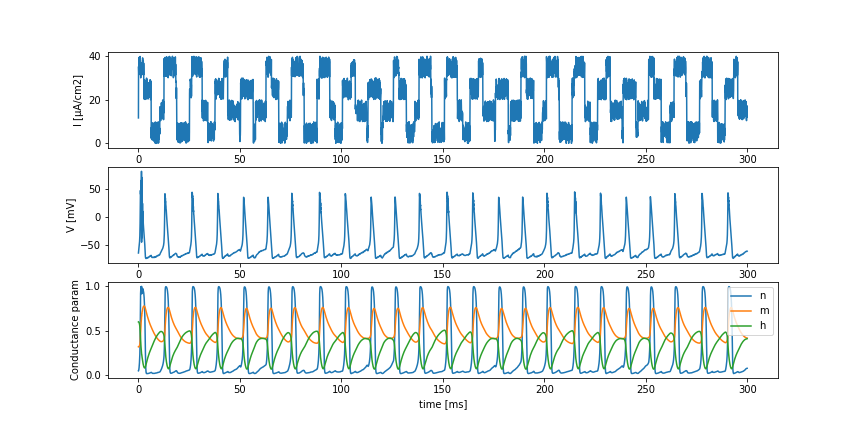
本モデルも適当な入力電流を与えてみます.
import numpy as np
import matplotlib.pyplot as plt
class HodgkinHuxley:
def __init__(self, time, dt, rest=-65., Cm=1.0, gNa=120., gK=36., gl=0.3, ENa=50., EK=-77., El=-54.387):
"""
Initialize Neuron parameters
:param time: experimental time
:param dt: time step
:param rest: resting potential
:param Cm: membrane capacity
:param gNa: Na+ channel conductance
:param gK: K+ channel conductance
:param gl: other (Cl) channel conductance
:param ENa: Na+ equilibrium potential
:param EK: K+ equilibrium potential
:param El: other (Cl) equilibrium potentials
"""
self.time = time
self.dt = dt
self.rest = rest
self.Cm = Cm
self.gNa = gNa
self.gK = gK
self.gl = gl
self.ENa = ENa
self.EK = EK
self.El = El
def calc(self, i):
""" compute membrane potential """
# initialize parameters
v = self.rest
n = 0.32
m = 0.05
h = 0.6
v_monitor = []
n_monitor = []
m_monitor = []
h_monitor = []
time = int(self.time / self.dt)
# update time
for t in range(time):
# calc channel gating kinetics
n += self.dn(v, n)
m += self.dm(v, m)
h += self.dh(v, h)
# calc tiny membrane potential
dv = (i[t] -
self.gK * n**4 * (v - self.EK) - # K+ current
self.gNa * m**3 * h * (v - self.ENa) - # Na+ current
self.gl * (v - self.El)) / self.Cm # other current
# calc new membrane potential
v += dv * self.dt
# record
v_monitor.append(v)
n_monitor.append(n)
m_monitor.append(m)
h_monitor.append(h)
return v_monitor, n_monitor, m_monitor, h_monitor
def dn(self, v, n):
return (self.alpha_n(v) * (1 - n) - self.beta_n(v) * n) * self.dt
def dm(self, v, m):
return (self.alpha_m(v) * (1 - m) - self.beta_m(v) * m) * self.dt
def dh(self, v, h):
return (self.alpha_h(v) * (1 - h) - self.beta_h(v) * h) * self.dt
def alpha_n(self, v):
return 0.01 * (10 - (v - self.rest)) / (np.exp((10 - (v - self.rest))/10) - 1)
def alpha_m(self, v):
return 0.1 * (25 - (v - self.rest)) / (np.exp((25 - (v - self.rest))/10) - 1)
def alpha_h(self, v):
return 0.07 * np.exp(-(v - self.rest) / 20)
def beta_n(self, v):
return 0.125 * np.exp(-(v - self.rest) / 80)
def beta_m(self, v):
return 4 * np.exp(-(v - self.rest) / 18)
def beta_h(self, v):
return 1 / (np.exp((30 - (v - self.rest))/10) + 1)
if __name__ == '__main__':
# init experimental time and time-step
time = 300 # 実験時間 (観測時間)
dt = 2**-4 # 時間分解能 (HHモデルは結構小さめでないと上手く計算できない)
# Hodgkin-Huxley Neuron
neuron = HodgkinHuxley(time, dt)
# 入力データ (面倒臭いので適当な矩形波とノイズを合成して作った)
input_data = np.sin(0.5 * np.arange(0, time, dt))
input_data = np.where(input_data > 0, 20, 0) + 10 * np.random.rand(int(time/dt))
input_data_2 = np.cos(0.4 * np.arange(0, time, dt) + 0.5)
input_data_2 = np.where(input_data_2 > 0, 10, 0)
input_data += input_data_2
# 膜電位などを計算
v, m, n, h = neuron.calc(input_data)
# plot
plt.figure(figsize=(12, 6))
x = np.arange(0, time, dt)
plt.subplot(3, 1, 1)
plt.plot(x, input_data)
plt.ylabel('I [μA/cm2]')
plt.subplot(3, 1, 2)
plt.plot(x, v)
plt.ylabel('V [mV]')
plt.subplot(3, 1, 3)
plt.plot(x, n, label='n')
plt.plot(x, m, label='m')
plt.plot(x, h, label='h')
plt.xlabel('time [ms]')
plt.ylabel('Conductance param')
plt.legend()
plt.show()このように,発火閾値を静的に定めなくとも脱分極と過分極が再現できていることがわかります.
しかし,これでは計算が複雑すぎて,やはり実用的ではありませんね.
3-4. Izhikevichニューロンモデル
最後に紹介するニューロンモデルは比較的新しいIzhikevichニューロンモデル [4]です.
Izhikevichニューロンモデルは,HHよりもかなりシンプルなモデルであるにもかかわらず,様々なニューロンの挙動を再現できるモデルとして多くの研究で取り上げられています.
本モデルは以下の式で表されます.
表記は他のモデルと違いますが,$v$は膜電位です.
$u$は回復変数(Recovery variable)と呼ばれる変数です.
上記の式を紐解くと,$(a,b,c,d)$という4つのパラメータと,$(v,t,u,I)$という4つの変数で成り立つ大変美しい式です.
それぞれの変数については,
- $a$ ... $u$のスケーリング係数
- $b$ ... $v$に対する$u$の感受性
- $c$ ... 静止膜電位
- $d$ ... 発火後に平衡状態に戻るまでの時間に影響する定数
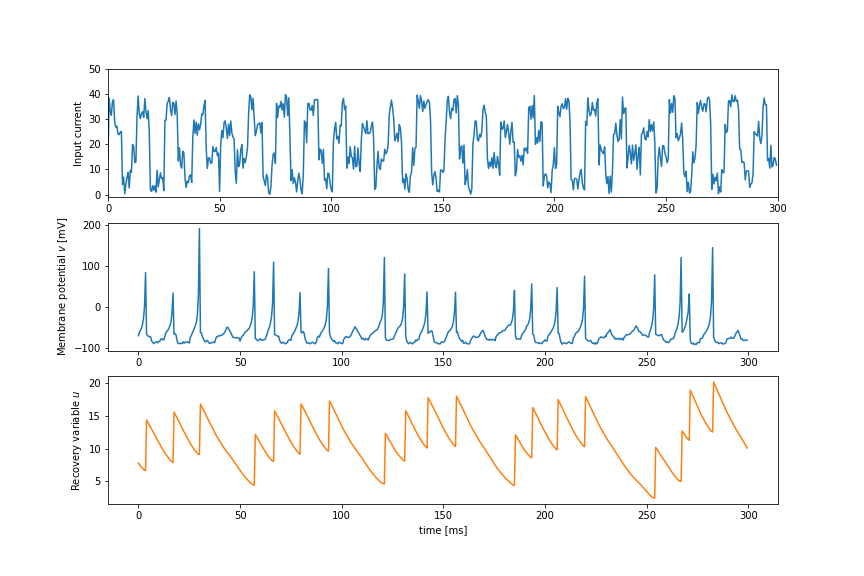
こちらも実際に挙動を見てみましょう.
import numpy as np
import matplotlib.pyplot as plt
class Izhikevich:
def __init__(self, a, b, c, d):
"""
Izhikevich neuron model
:param a: uのスケーリング係数
:param b: vに対するuの感受性度合い
:param c: 静止膜電位
:param d: 発火後の膜電位が落ち着くまでを司る係数
"""
self.a = a
self.b = b
self.c = c
self.d = d
def calc(self, inputs, time=300, dt=0.5, tci=10):
"""
膜電位(Membrane potential) v と回復変数(Recovery variable) u を計算する
:param inputs:
:param weights:
:param time:
:param dt:
:param tci:
:return:
"""
v = self.c
u = self.d
i = 0
monitor = {'v': [], 'u': []}
for t in range(int(time/dt)):
# uを計算
du = self.a * (self.b * v - u)
u += du * dt
monitor['u'].append(u)
# vを計算
dv = 0.04 * v**2 + 5 * v + 140 - u + inputs[t]
v += dv * dt
monitor['v'].append(v)
# 発火処理
if v >= 30:
v = self.c
u += self.d
return monitor
if __name__ == '__main__':
time = 300 # 実験時間 (観測時間)
dt = 0.5 # 時間分解能
pre = 50 # 前ニューロンの数
# 入力データ (面倒臭いので適当な矩形波とノイズを合成して作った)
input_data = np.sin(0.5 * np.arange(0, time, dt))
input_data = np.where(input_data > 0, 20, 0) + 10 * np.random.rand(int(time/dt))
input_data_2 = np.cos(0.4 * np.arange(0, time, dt) + 0.5)
input_data_2 = np.where(input_data_2 > 0, 10, 0)
input_data += input_data_2
# Izhikevichニューロンの生成 (今回はRegular Spiking Neuronのパラメータ)
neuron = Izhikevich(
a=0.02,
b=0.2,
c=-65,
d=8
)
history = neuron.calc(input_data, time=time, dt=dt)
# 結果の描画
plt.figure(figsize=(12, 8))
# 入力データ
plt.subplot(3, 1, 1)
plt.plot(t, input_data)
plt.xlim(0, time)
plt.ylim(-1, pre)
plt.ylabel('Input current')
# 膜電位
plt.subplot(3, 1, 2)
plt.plot(t, history['v'])
plt.ylabel('Membrane potential $v$ [mV]')
# 膜電位
plt.subplot(3, 1, 3)
plt.plot(t, history['u'], c='tab:orange')
plt.xlabel('time [ms]')
plt.ylabel('Recovery variable $u$')
plt.show()上記の例では,Regular Spiking Neuronと呼ばれるニューロンのシミュレーションをしてみました.
どの挙動をシミュレーションするかは,パラメータ$(a,b,c,d)$によって決まるので色々と試してみると良いでしょう.
なおWeb上で簡単にIzhikevichニューロンの挙動を観察できるサイトを昔作ったのでぜひ遊んでみてください.
Izhikevichニューロンモデルはカオスの観察もできるモデルなので,工学的研究に止まらず,神経科学分野でも広く使われているモデルです.
- ちなみにカオス(Chaos)をシミュレーションしてみると...
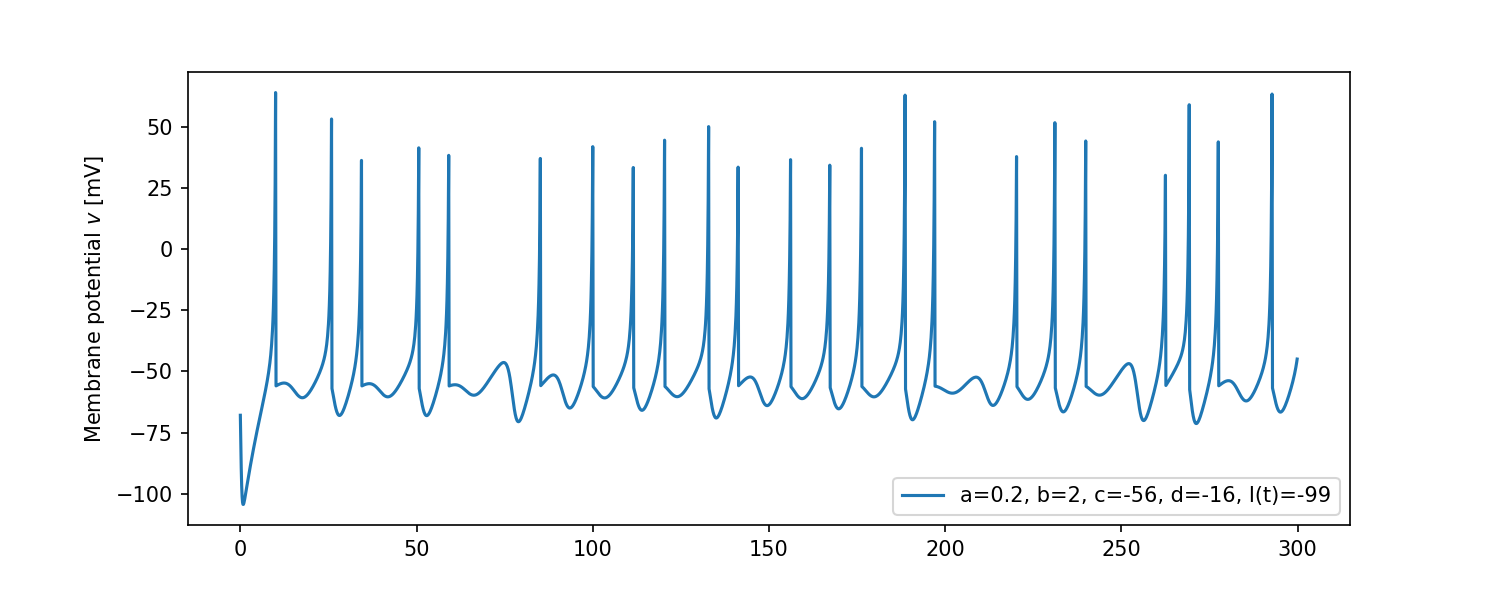
こんな感じ. 一定の負の入力電流に対して不規則な発火(カオス)が観測できる.($dt=0.125$以下がベスト)
3-5. 入力電流の計算
さて,今まで紹介してきたスパイキングニューロンモデルは全て入力を電流として定義しました.
しかし何度も言うように,実際に細胞に入力されるのは{0,1}のスパイク列です.
本節では,スパイク列 ⇨ 入力電流への変換について紹介していきます.
デジタル信号をアナログ信号に変換する上で,最も単純なアイデアは信号の畳み込みです.
信号の畳み込みについてイマイチ分からない人に向けて,試しにNumPyの
convolve()
関数で畳み込みのイメージを掴みましょう.
import numpy as np
import matplotlib.pyplot as plt
def kernel(t):
""" 畳み込みカーネル """
return np.exp(-t / 20) - np.exp(-t / 10)
if __name__ == '__main__':
# 観測時間とタイムステップ
time = 100
dt = 0.5
# もともとのデジタル信号を適当に作る
spikes = np.zeros(int(time / dt))
spikes[50] = 1
spikes[70] = 1
spikes[140] = 1
t = np.arange(0, time, dt)
plt.figure(figsize=(14, 4))
plt.subplot(1, 3, 1)
plt.title(r'Original Spike Train $s(t)$')
plt.plot(t, spikes)
plt.xlabel('time [ms]')
plt.subplot(1, 3, 2)
plt.title(r'Conv. Kernel $H(t)$')
plt.plot(t, kernel(t))
plt.xlabel('time [ms]')
plt.subplot(1, 3, 3)
plt.title(r'Result: $s(t) * H(t)$')
plt.plot(t, np.convolve(spikes, kernel(t))[:int(time / dt)])
plt.xlabel('time [ms]')
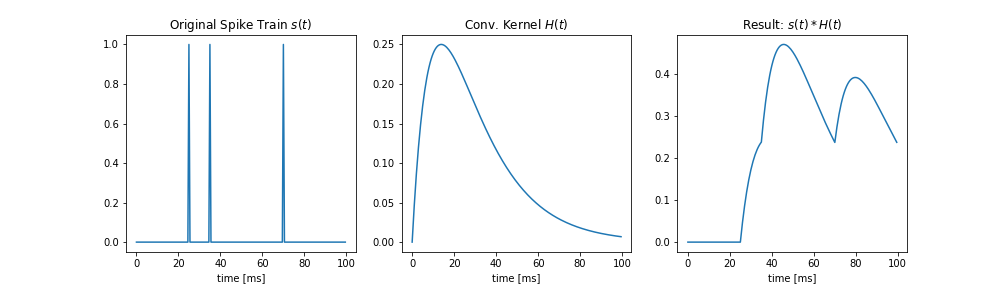
plt.show()こんな感じ.
上の例では,2つの指数関数からなるカーネルを用いました.(Double Exponential Kernel)
が,実際はプログラミングしやすい1つの指数関数からなるカーネルがよく使われます.(Single Exponential Kernel)
なぜ扱いやすいかと言うと,単純な微分方程式で表すことができ,膜電位の計算と同時に行うことができるからです.
何を言っているんだ,と思うかもしれませんが要するに,
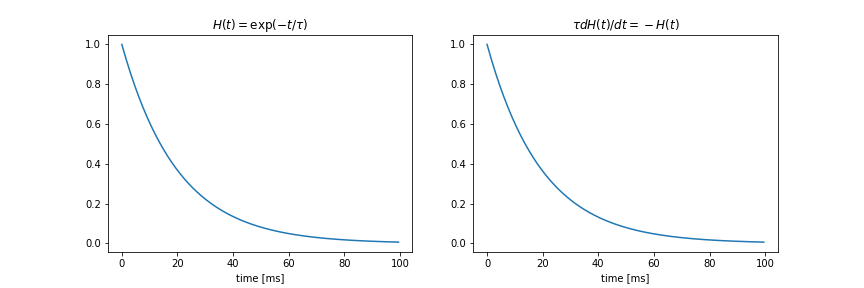
$$H(t) = \exp(-t / \tau)$$
$$\tau\frac{dH(t)}{dt} = -H(t)$$
は同じ物ということです.
試しにプログラムで書いてみましょう.
import numpy as np
import matplotlib.pyplot as plt
def single_exp(t):
return np.exp(-t / 20)
if __name__ == '__main__':
# 観測時間とタイムステップ
time = 100
dt = 0.5
h = 1 # 初期値
result = []
# 微分法定式を解く
for t in range(int(time / dt)):
result.append(h)
dh = -h * dt # dH = -H · dt
h += dh / 20 # h ← h + dh / τ
t = np.arange(0, time, dt)
plt.figure(figsize=(12, 4))
plt.subplot(1, 2, 1)
plt.plot(t, single_exp(t))
plt.title(r'$H(t) = \exp(-t / \tau)$')
plt.xlabel('time [ms]')
plt.subplot(1, 2, 2)
plt.plot(t, result)
plt.title(r'$\tau dH(t) / dt = -H(t)$')
plt.xlabel('time [ms]')
plt.show()
言っていることが伝わりましたか?
この手の話は,微分方程式をよく知らない人には理解に時間がかかりますが,実際に紙に書いたり手計算してみると理解が深まると思います.
そして話は戻りますが,神経細胞への入力はスパイク列ですので,この方法を用いて変換式を立てると以下のようになります.
$$\tau_{i}\frac{dI(t)}{dt} = -I(t) + \sum_{i\in N}{w_{i}\cdot s_{i}(t)}$$
ここで,$-I(t)$の部分が指数関数的減衰として機能します.
その後ろの項は,シナプス前ニューロン全ての重み$w$とスパイク一本一本をそれぞれかけて足し合わせてるだけです.
$s(t)$は,時刻$t$にスパイクがあれば$1$を,なければ$0$を返す関数です.
しっかり詳細に書いてある論文では以下のような式で表したりしています.
$$s(t) = \sum_{t^{f}\in \Gamma}{\delta(t-t^f)}$$
$\Gamma$は発火時刻集合で,$\delta(t)$はディラックのデルタ関数です.
この辺りも,紙に描きながら理解すると良いでしょう.
次はエンコーディングについてですが,今回の話を踏まえて次章最後に実装例を載せますので,入力電流についての話は一旦終わりです.
